Abstract
The success of multi-head self-attentions (MSAs) for computer vision is now indisputable. However, little is known about how MSAs work. We present fundamental explanations to help better understand the nature of MSAs. In particular, we demonstrate the following properties of MSAs and Vision Transformers (ViTs): (1) MSAs improve not only accuracy but also generalization by flattening the loss landscapes. Such improvement is primarily attributable to their data specificity, not long-range dependency. On the other hand, ViTs suffer from non-convex losses. Large datasets and loss landscape smoothing methods alleviate this problem; (2) MSAs and Convs exhibit opposite behaviors. For example, MSAs are low-pass filters, but Convs are high-pass filters. Therefore, MSAs and Convs are complementary; (3) Multi-stage neural networks behave like a series connection of small individual models. In addition, MSAs at the end of a stage play a key role in prediction. Based on these insights, we propose AlterNet, a model in which Conv blocks at the end of a stage are replaced with MSA blocks. AlterNet outperforms CNNs not only in large data regimes but also in small data regimes. The code is available at this https URL.
Notes
The question of inductive biases
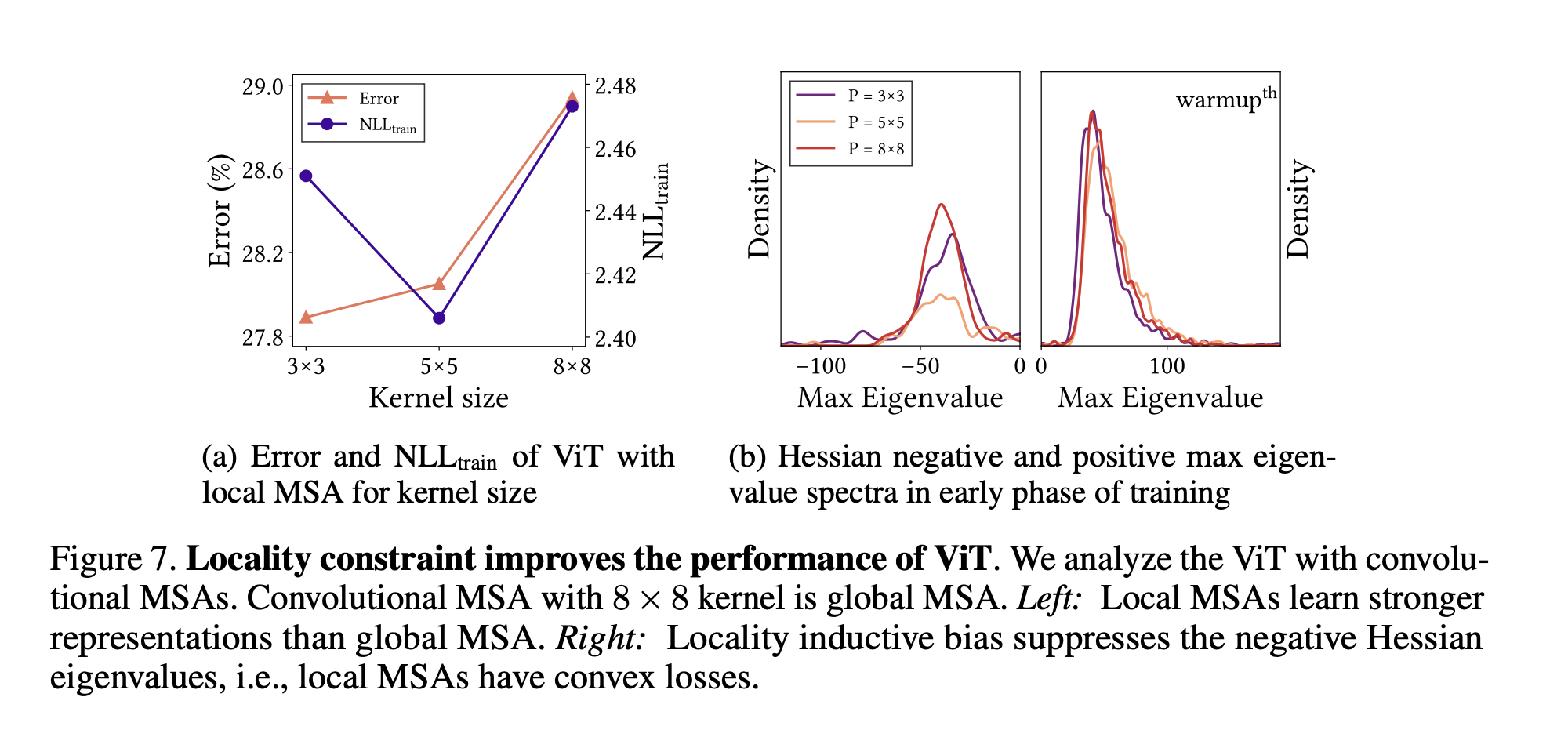
Contrary to our expectations, experimental results show that the stronger the inductive bias, the lower both the test error and the training NLL. This indicates that ViT does not overfit training datasets. In addition, appropriate inductive biases, such as locality constraints for MSAs, helps NNs learn strong representations. We also observe these phenomena on CIFAR-10 and ImageNet as shown in Fig. C.1. Figure C.2 also supports that weak inductive biases disrupt NN training. In this experiment, extremely small patch sizes for the embedding hurt the predictive performance of ViT.
Long range (global) attention is worse than local attention. MSA are good because they smooth loss landscape and are input dependent.
What properties of MSAs do we need to improve optimization? We present various evidences to support that MSA is generalized spatial smoothing. It means that MSAs improve performance because their formulation—Eq. (1)—is an appropriate inductive bias. Their weak inductive bias disrupts NN training. In particular, a key feature of MSAs is their data specificity, not long-range dependency. As an extreme example, local MSAs with a 3 × 3 receptive field outperforms global MSA because they reduce unnecessary degrees of freedom.
As far as my understanding goes, local MSA is not translation equivariant because it still is input dependent. So Local MSA has locality inductive bias but not translation equivariance. This is interesting, normal ConvNets do locality inductive bias by translation equivariance and it is not straight forward to remove their translation equivariance. Tracking at Input-dependent convolutions and Non-translationally equivariant convolutions.
Locality inductive biases help with more stable training dynamics
Hessian Spectra
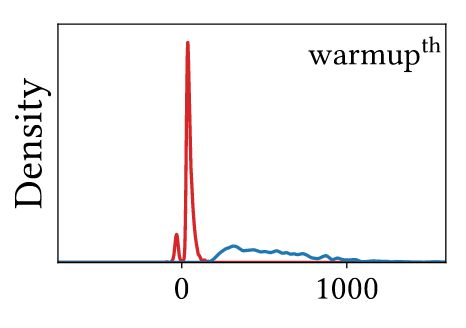Legend: ViT (red), CNN (blue)
- ViT has small magnitude and negative values
- CNN has large magnitude and positive values